Číselné soustavy, reprezentace celých čísel
V seriálu O programování obecně se věnujeme tématům, která by měl každý programátor znát. Většinu z informací, které ve článcích najdete, můžete využít jak při programování Arduina, tak i v jiných programovacích jazycích. V následujících článcích se budeme věnovat datovým typů. K jejich snazšímu pochopení si ale nejdříve vysvětlíme číselné soustavy.
Pro počítač jsou všechny hodnoty pouhá čísla. Protože počítač pracuje v binární (dvojkové) soustavě, jsou to nuly a jedničky. To až programátor svým programem dává číslům nějaký význam a podle toho s nimi také manipuluje.
Existují různé číselné soustavy. My jsme běžně zvyklí počítat v desítkové soustavě (máme deset číslic: 0 až 9). Jedny z prvních počítačů byly založené na desítkové soustavě. Ukázalo se ale, že to není dobrá cesta. Vedle počítačů založených na desítkové soustavě vznikaly také počítače pracující s binární soustavou, která se uchytila. Je totiž daleko jednodušší rozlišit mezi dvěma stavy napětí na vodiči (0V – logická nula, 5V – logická jednička), než rozlišovat mezi stavy deseti. Při programování se setkáme ještě se soustavou šestnáctkovou, která používá pro zápis čísel šestnáct znaků – 0 až 9 a A až F. Ta se využívá kvůli zkrácení zápisu dvojkových čísel. Navíc je převod mezi dvojkovou a šestnáctkovou soustavou snazší, než převod mezi dvojkovou a desítkovou.
Obsah článku:
Dvojková soustava
Ve dvojkové soustavě si máme k dispozici pro vyjádření čísel pouze dvě číslice – jsou to nula a jednička.
Převod z dvojkové na desítkovou soustavu
Začneme pozpátku převodem čísla v dvojkové soustavě na číslo v desítkové. Ve dvojkové soustavě můžeme použít k zápisu čísla pouze dvě číslice – 0 nebo 1. Mějme tedy například číslo zapsané ve dvojkové soustavě následovně:
(01101101)2
Toto číslo má celkem osm bitů (číslic), tvoří tedy jeden byte. K převodu do desítkové soustavy potřebujeme znát mocniny dvojky. Ty naleznete v tabulce níže, která je úmyslně zapsaná pozpátku.
| x | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| 2x | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
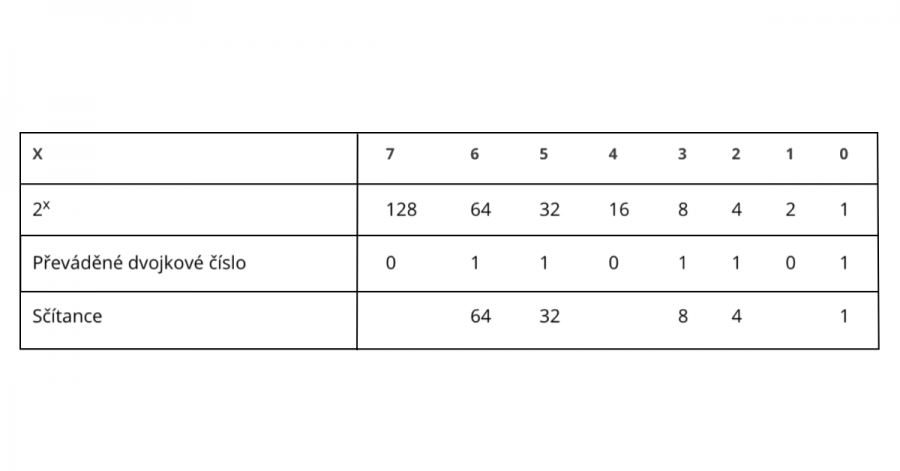
Výslednou hodnotu tvoříme jako součet mocnin dvojky na jednotlivých pozicích – pokud je na pozici 0, hodnotu nepřičteme, pokud 1, hodnotu přičteme. Číslice s největší hodnotou je vlevo, s nejmenší vpravo (proto jsou také mocniny zapsané pozpátku).
| x | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| 2x | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Převáděné dvojkové číslo | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| Sčítance | 64 | 32 | 8 | 4 | 1 |
Výsledné číslo tedy získáme jako součet 64 + 32 + 8 + 4 + 1 = 109. To by bylo jednoduché. Jak na opačný směr?
Převod z desítkové na dvojkovou soustavu
Nyní musíme postupovat přesně opačně – tedy zjistit, kam do výsledného dvojkového čísla zapsat jedničky a kam nuly. Převod si opět vysvětlíme na příkladu. Mějme desítkové číslo
(105)10
Na začátku zjistíme, která nejvyšší mocnina dvojky se do čísla vejde. Zapíšeme si jedničku, mocninu od čísla odečteme a zkoumáme, jestli se do výsledku vejde následující menší mocnina. Pokud ne, píšeme 0, pokud ano, píšeme 1. Mocninu od čísla odečítáme jen v případě, že jsme ji „použili“. Tedy pro naše číslo:
- Nejvyšší mocnina dvou, která se do 105 vejde je 64. Zapíšeme 1. 105 – 64 = 41
- Následující mocnina je 32, ta se do 41 vejde. Píšeme 1. 41 – 32 = 9.
- Následující mocnina je 16, ta se do 9 nevejde. Píšeme 0.
- Následující mocnina je 8, ta se do 9 vejde. Píšeme 1. 9 – 8 = 1
- Následující mocnina je 4, ta se do 1 nevejde. Píšeme 0.
- Následující mocnina je 2, ta se do 1 nevejde. Píšeme 0.
- Poslední mocnina je 1. Ta se do do 1 vejde. Píšeme 1 a náš převod končí.
Výsledným číslem je (1101001)2. To je 7 bitů. Pokud bychom chtěli vytvořit celý byte, přidáme před číslo 0. Výsledek tedy bude (01101001)2.
Existuje ještě jeden způsob založený na zaznamenávání zbytků po dělení 2. U něj dvojkové číslo tvoříme z opačného konce. Ukážeme si opět příklad s převodem čísla 105.
- 105 / 2 = 52, zbytek 1
- 52 / 2 = 26, zbytek 0
- 26 / 2 = 13, zbytek 0
- 13 / 2 = 6, zbytek 1
- 6 / 2 = 3, zbytek 0
- 3 / 2 = 1, zbytek 1
- 1 / 2 = 0, zbytek 1 a převod končí
Zde pozor na pořadí číslic. Je opačné než u předchozího způsobu. Výsledek je tedy opět (1101001)2. Oba popsané způsoby jsou ekvivalentní a záleží na preferenci každého, který bude využívat.
Zápis binárních čísel v C/C++
V C/C++ jako takovém nemáme možnost, jak zapsat binární konstantu přímo. Arduino přináší některé předdefinované binární konstanty, které můžeme v programu použít. Jsou to:
B00000000 až B11111111
Tedy například
int a = B11110010;
Osmičková soustava
Touto soustavou se moc zabývat nebudeme. Je ale potřeba si dát pozor na to, jak zapisujeme čísla. Pokud máme celé číslo začínající nulou, překladač ho bere jako číslo v osmičkové soustavě. Platí tedy, že
0123 != 123
protože 0123 je zapsané v osmičkové, kdežto 123 v desítkové soustavě.
Šestnáctková soustava
Šestnáctková (hexadecimální) soustava se při programování používá celkem často, protože je jednoduše převoditelná do dvojkové a zároveň je zápis čísel v ní o hodně kratší. Převod z dvojkové soustavy do šestnáctkové probíhá tak, že si dvojkové číslo rozdělíme do čtveřic bytů, které poté převádíme na jednotlivé číslice šestnáctkové soustavy. Ty mají hodnotu podle následující tabulky:
| šestnáctková číslice | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| hodnota v desítkové soustavě | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Máme-li šestnáctibitové číslo ve dvojkové soustavě (1001010100001011)2, převedeme ho do šestnáctkové tak, že ho rozdělíme do čtveřic bitů a ty poté převádíme.
| dvojkově | 1001 | 1101 | 0000 | 1011 |
| desítkově | 9 | 13 | 0 | 11 |
| šestnáctkově | 9 | D | 0 | B |
Výsledná číslice v šestnáctkové soustavě je tedy 9D0B. Abychom zápis odlišili od čísel v desítkové soustavě, předáváme před šestnáctková čísla 0x, tedy výsledný zápis bude 0x9D0B. Převod z šestnáctkové do dvojkové soustavy probíhá přesně opačně. V C/C++ zapíšeme číslo v šestnáctkové soustavě do proměnné takto:
int a = 0xF2;
Reprezentace celých čísel v paměti procesorů
Celá čísla dělíme podle toho, jestli jsou znaménková, nebo bezznaménková. Znaménkové číslo může reprezentovat jak kladné, tak záporné hodnoty. Bezznaménkové číslo reprezentuje hodnoty od nuly výše.
Pokud máme proměnnou o velikosti jeden byte (tedy osm bitů), máme k dispozici celkem 256 hodnot. Pokud v něm chceme uchovávat zápornou hodnotu, musíme použít znaménkový datový typ. Celkový rozsah si rozdělíme na dvě poloviny – jedna bude reprezentovat hodnoty 0 až 127 (128 hodnot) a druhá -1 až -128 (také 128 hodnot). Stejný postup bychom zvolili i kdybychom měli proměnnou o velikosti 2, nebo 4 byty.
Hodnoty v kladné polovině převádíme z desítkové do dvojkové soustavy tak, jak jsme si to představili dříve. Záporné hodnoty se ale převádějí odlišně. Pro procesory je nejvhodnější reprezentovat záporná čísla v tzv. dvojkovém doplňku. Ten získáme následovně:
- Vytvoříme absolutní hodnotu ze záporného čísla
- Absolutní hodnotu převedeme na číslo ve dvojkové soustavě
- Všechny bity v získaném dvojkovém vyjádření znegujeme (z 0 uděláme 1 a naopak)
- Přičteme jedničku
- Takto jsme získali binární zápis záporného čísla pomocí dvojkového doplňku
Mějme kupříkladu číslo (-1)10.
- Absolutní hodnota z -1 je 1
- (1)10 zapíšeme binárně na osmi bitech jako (00000001)2
- bitovou negací (00000001)2 získáme (11111110)2
- (11111110)2 + (00000001)2 = (11111111)2
- (-1)10 = (11111111)2
Číslo (-1)10 tedy zapíšeme pomocí dvojkového doplňku jako (11111111)2.
To by bylo pro dnešek všechno. V příštím článku z tohoto seriálu si představíme celočíselné datové typy, které můžeme při programování Arduina použít.
- Programovatelný kytarový pedál s Arduinem - 26.2.2020
- Arduino infračervený teploměr vytištěný na 3D tiskárně - 11.2.2020
- Jak je to s IP, MAC adresami a sítěmi - 18.12.2019
